College Algebra
Topic outline
-
Welcome to College Algebra [CMAT 1213]!
Course Introduction
This College Algebra [CMAT 1213] course adheres to the scope and sequence of a one-semester College Algebra course. The course description provided is the from the statewide common course information.Course Description: In-depth treatment of solving equations and inequalities; function properties and graphs; inverse functions; linear, quadratic, polynomial, rational, exponential and logarithmic functions with applications; systems of equations.
Upon successful completion of this course, the student will be able to:
- Solve equations and inequalities.
- Graph and analyze mathematical functions.
-
- Model and solve application problems.
Adopting instructors can embed a welcome video or add additional text here.
Structure of the CourseThe course includes 6 content Modules which covers each of the 6 chapters in the textbook (provided link). Each module includes a brief introduction text with module learning objectives, links to the corresponding Pressbook sections, homework assignments in MyOpenMath, a Chapter Review with Exercises, a Chapter Practice Test, a Quiz in MyOpenMath, and a Q&A discussion forum for that Module. There are additional modules for smaller Exams, a Midterm Exam, and/or Final Exam.
Navigating the Course
This course is set up in Modules covering various topics which may be accessed from the course navigation menu on the left or by scrolling below. Modules may be collapsed in the menu and it the body of the course to minimize scrolling. Many items are required and may be marked as completed automatically when the activity has been submitted (the broken check box), but others will marked as done by the student (the solid check box).
Please move through the items below and continue through the Learner Support and Getting Started modules before moving on to Module 1. Be sure to check for announcements and due dates to stay on track.Adopting instructors can embed a navigation video or add additional text here.
This course and its contents are licensed under a Creative Commons Attribution 4.0 International License by LOUIS: The Louisiana Library Network, except where otherwise noted. Adopting instructors should edit the About Your Instructor and Office Hours Information pages in this Module.
-
Adopting instructors should edit all pages in this Module - as per their own Institution's policies.
-
This module contains all the items you should review and complete before you begin Module 1. Before moving on, be sure to:
- Check the News and Announcements Forum
- Read the Course Syllabus
- Introduce yourself to the class
- Read the instructions for the Q & A Forum
Good luck in the course!-
This forum contains general news and announcements. You can find all announcements listed in the "Latest News" block in Course Tools within this course or on your My Courses page.
-
Students mustMark as done
Use this forum to tell us a little about yourself and your interests. Some topic ideas:
- What is your field of study/research interest or concentration?
- What are you most interested in learning about in this class and why?
- Have you ever taken an online class before?
- Any other information you would like to share with your classmates, such as special interests or activities.
Post a picture! We look forward to meeting you.
-
Students mustMark as done
Use this forum to ask your instructor any questions you have about the course. You may post at any time, and your instructor will respond here. Be as specific as possible.
Please keep in mind that others can see your posts, so do not post any personal information. If you have questions about your grade, please email your instructor directly. You can expect a response to posts and emails within [X] hours. [Recommendation is 24 hours M-F, next business day on weekends.]
Subscription should be set to Auto.
-
This forum contains general news and announcements. You can find all announcements listed in the "Latest News" block in Course Tools within this course or on your My Courses page.
-
Students mustMark as done
Use this forum to tell us a little about yourself and your interests. Some topic ideas:
- What is your field of study/research interest or concentration?
- What are you most interested in learning about in this class and why?
- Have you ever taken an online class before?
- Any other information you would like to share with your classmates, such as special interests or activities.
Post a picture! We look forward to meeting you.
-
Students mustMark as done
Use this forum to ask your instructor any questions you have about the course. You may post at any time, and your instructor will respond here. Be as specific as possible.
Please keep in mind that others can see your posts, so do not post any personal information. If you have questions about your grade, please email your instructor directly. You can expect a response to posts and emails within [X] hours. [Recommendation is 24 hours M-F, next business day on weekends.]
Subscription should be set to Auto.
-
This forum contains general news and announcements. You can find all announcements listed in the "Latest News" block in Course Tools within this course or on your My Courses page.
-
Students mustMark as done
Use this forum to tell us a little about yourself and your interests. Some topic ideas:
- What is your field of study/research interest or concentration?
- What are you most interested in learning about in this class and why?
- Have you ever taken an online class before?
- Any other information you would like to share with your classmates, such as special interests or activities.
Post a picture! We look forward to meeting you.
-
Students mustMark as done
Use this forum to ask your instructor any questions you have about the course. You may post at any time, and your instructor will respond here. Be as specific as possible.
Please keep in mind that others can see your posts, so do not post any personal information. If you have questions about your grade, please email your instructor directly. You can expect a response to posts and emails within [X] hours. [Recommendation is 24 hours M-F, next business day on weekends.]
Subscription should be set to Auto.
-
This forum contains general news and announcements. You can find all announcements listed in the "Latest News" block in Course Tools within this course or on your My Courses page.
-
Students mustMark as done
Use this forum to tell us a little about yourself and your interests. Some topic ideas:
- What is your field of study/research interest or concentration?
- What are you most interested in learning about in this class and why?
- Have you ever taken an online class before?
- Any other information you would like to share with your classmates, such as special interests or activities.
Post a picture! We look forward to meeting you.
-
Students mustMark as done
Use this forum to ask your instructor any questions you have about the course. You may post at any time, and your instructor will respond here. Be as specific as possible.
Please keep in mind that others can see your posts, so do not post any personal information. If you have questions about your grade, please email your instructor directly. You can expect a response to posts and emails within [X] hours. [Recommendation is 24 hours M-F, next business day on weekends.]
Subscription should be set to Auto.
- Check the News and Announcements Forum
-
It’s a cold day in Antarctica. In fact, it’s always a cold day in Antarctica. The coldest temperature ever recorded, over one hundred degrees below zero on the Celsius scale, was recorded by remote satellite. It is no surprise then, that no native human population can survive the harsh conditions. Only explorers and scientists brave the environment for any length of time.
Measuring and recording the characteristics of weather conditions in Antarctica requires a use of different kinds of numbers. For tens of thousands of years, humans have undertaken methods to tally, track, and record numerical information. While we don't know much about their usage, the Lebombo Bone (dated to about 35,000 BCE) and the Ishango Bone (dated to about 20,000 BCE) are among the earliest mathematical artifacts. Found in Africa, their clearly deliberate groupings of notches may have been used to track time, moon cycles, or other information. Performing calculations with them and using the results to make predictions requires an understanding of relationships among numbers. In this chapter, we will review sets of numbers and properties of operations used to manipulate numbers. This understanding will serve as prerequisite knowledge throughout our study of algebra.
Image Caption: Earth’s southernmost continent, Antarctica experiences the coldest, driest, and windiest conditions known. (Credit: Andreas Kambanls)
(Content & Image Source: Chapter 1 Introduction, Algebra and Trigonometry 2e, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:Section 1.1 Real Numbers: Algebra Essentials
- Classify a real number as a natural, whole, integer, rational, or irrational number. (CLO #)
- Perform calculations using order of operations.
- Use the following properties of real numbers: commutative, associative, distributive, inverse, and identity.
- Evaluate algebraic expressions.
- Simplify algebraic expressions.
Section 1.2 Exponents and Scientific Notation
- Use the product rule of exponents.
- Use the quotient rule of exponents.
- Use the power rule of exponents.
- Use the zero exponent rule of exponents.
- Use the negative rule of exponents.
- Find the power of a product and a quotient.
- Simplify exponential expressions.
- Use scientific notation.
Section 1.3 Radicals and Rational Exponents
- Evaluate square roots.
- Use the product rule to simplify square roots.
- Use the quotient rule to simplify square roots.
- Add and subtract square roots.
- Rationalize denominators.
- Use rational roots.
Section 1.4 Polynomials
- Identify the degree and leading coefficient of polynomials.
- Add and subtract polynomials.
- Multiply polynomials.
- Perform operations with polynomials of several variables.
Section 1.5 Factoring Polynomials
- Factor the greatest common factor of a polynomial.
- Factor a trinomial.
- Factor by grouping.
- Factor a perfect square trinomial.
- Factor a difference of squares.
- Factor the sum and difference of cubes.
- Factor expressions using fractional or negative exponents.
Section 1.6 Rational Expressions
- Simplify rational expressions.
- Multiply rational expressions.
- Divide rational expressions.
- Add and subtract rational expressions.
- Simplify complex rational expressions.
To achieve these objectives:- Read the Module 1 Introduction (see above).
- Read Sections 1.1 - 1.6 of Chapter 1: Prerequisites in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 1 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 1 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 1 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 1 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
For most people, the term territorial possession indicates restrictions, usually dealing with trespassing or rite of passage and takes place in some foreign location. What most Americans do not realize is that from September through December, territorial possession dominates our lifestyles while watching the NFL. In this area, territorial possession is governed by the referees who make their decisions based on what the chains reveal. If the ball is at point A (x1, y1) then it is up to the quarterback to decide which route to point B (x2, y2) the end zone, is most feasible.
Image Caption: A large orange circle with an arrow printed on it facing to the right atop a rectangular base, known as chains in football, is shown prominently in the foreground. In the background there is a game of football ongoing with fans in their seats. (Credit: Jeramey Jannene, Flickr)
(Content & Image Source: Chapter 2 Introduction, Algebra and Trigonometry, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:Section 2.1 Linear Equations in One VariableSection 2.2 Models and Applications- Solve equations in one variable.
- Solve a rational equation.
Section 2.3 Complex Numbers- Set up a linear equation to solve a real-world application.
- Use a formula to solve a real-world application.
Section 2.4 Quadratic Equations- Add and subtract complex numbers.
- Multiply complex numbers.
- Divide complex numbers.
- Simplify powers of i
Section 2.5 Other Types of Equations- Solve quadratic equations by factoring.
- Solve quadratic equations by the square root property.
- Solve quadratic equations by completing the square.
- Solve quadratic equations by using the quadratic formula.
- Solve equations involving rational exponents.
- Solve equations using factoring.
- Solve radical equations.
- Solve absolute value equations.
- Solve other types of equations.
Section 2.6 Linear Inequalities and Absolute Value Inequalities- Write solutions using interval notation.
- Solve inequalities in one variable algebraically.
- Solve absolute value inequalities.
To achieve these objectives:- Read the Module 2 Introduction (see above).
- Read Sections 2.1 - 2.6 of Chapter 2: Equations and Inequalities in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 2 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 2 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 2 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 2 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.
Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
In this module you will take your Exam 1 . Read the Exam 1 Information and Instructions page carefully and take note of any special submission guidelines.
Upon completion of this module, you will have:- Read and viewed the Exam 1 Information and Instructions page
- Scheduled your exam with the proctoring service [if applicable, delete if not needed]
- Post in the Exam 1 Q&A Discussion Forum - link provided below.
- Prepared for and submitted your Exam 1 [revise as needed]
- Uploaded your work in the Exam 1 Work Upload Assignment using the submission link below.
Attribution of image: ("Math, Numbers, Number image. Free for use." Pixabay.com. https://pixabay.com/photos/math-numbers-number-counting-5247958/)
Adopting instructors: Edit the Exam 1 Information and Instructions page.
-
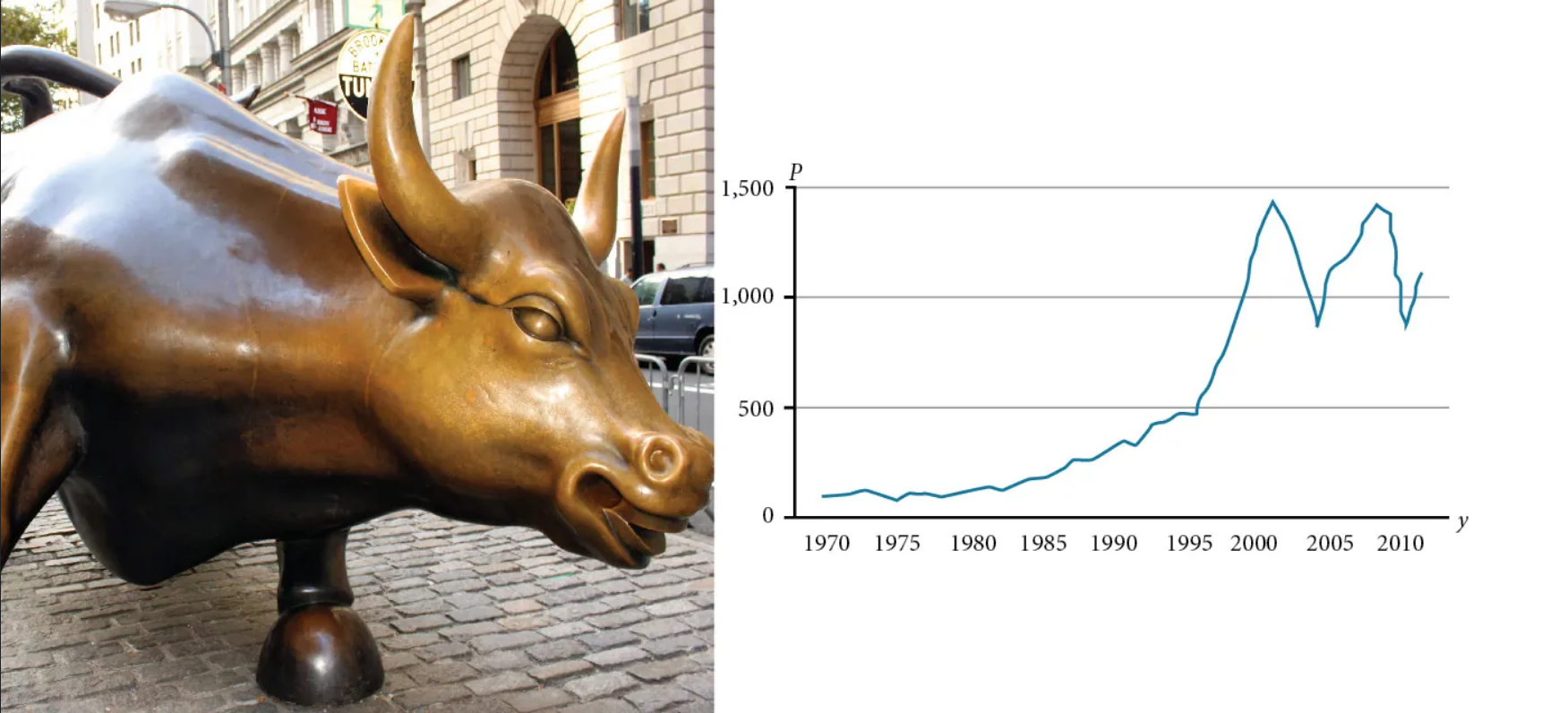
Toward the end of the twentieth century, the values of stocks of Internet and technology companies rose dramatically. As a result, the Standard and Poor’s stock market average rose as well. The graph above tracks the value of that initial investment of just under $100 over the 40 years. It shows that an investment that was worth less than $500 until about 1995 skyrocketed up to about $1100 by the beginning of 2000.
That five-year period became known as the “dot-com bubble” because so many Internet startups were formed. As bubbles tend to do, though, the dot-com bubble eventually burst. Many companies grew too fast and then suddenly went out of business. The result caused the sharp decline represented on the graph beginning at the end of 2000.
Notice, as we consider this example, that there is a definite relationship between the year and stock market average. For any year we choose, we can determine the corresponding value of the stock market average. In this chapter, we will explore these kinds of relationships and their properties.
Image Caption: Standard and Poor’s Index with dividends reinvested (credit "bull": modification of work by Prayitno Hadinata; credit "graph": modification of work by MeasuringWorth)
(Content & Image Source: Chapter 3 Introduction, Algebra and Trigonometry 2e, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:Section 3.1 The Rectangular Coordinate Systems and GraphsSection 3.2 Functions and Function Notation- Plot ordered pairs in a Cartesian coordinate system.
- Graph equations by plotting points.
- Graph equations with a graphing utility.
- Find x-intercepts and y-intercepts.
- Use the distance formula.
- Use the midpoint formula.
- Determine whether a relation represents a function.
- Find the value of a function.
- Determine whether a function is one-to-one.
- Use the vertical line test to identify functions.
- Graph the functions listed in the library of functions.
Section 3.3 Domain and RangeSection 3.4 Rates of Change and Behavior of Graphs- Find the domain of a function defined by an equation.
- Graph piecewise-defined functions.
Section 3.5 Composition of Functions- Find the average rate of change of a function.
- Use a graph to determine where a function is increasing, decreasing, or constant.
- Use a graph to locate local maxima and local minima.
- Use a graph to locate the absolute maximum and absolute minimum.
Section 3.6 Transformation of Functions- Combine functions using algebraic operations.
- Create a new function by composition of functions.
- Evaluate composite functions.
- Find the domain of a composite function.
- Decompose a composite function into its component functions.
Section 3.7 Absolute Value Functions- Graph functions using vertical and horizontal shifts.
- Graph functions using reflections about the ,x-axis and the y-axis.
- Determine whether a function is even, odd, or neither from its graph.
- Graph functions using compressions and stretches.
- Combine transformations.
Section 3.8 Inverse Functions- Graph an absolute value function.
- Solve an absolute value equation.
- Verify inverse functions.
- Determine the domain and range of an inverse function, and restrict the domain of a function to make it one-to-one.
- Find or evaluate the inverse of a function.
- Use the graph of a one-to-one function to graph its inverse function on the same axes.
To achieve these objectives:- Read the Module 3 Introduction (see above).
- Read Sections 3.1 - 3.8 of Chapter 3: Functions in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 3 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 3 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 3 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 3 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
In this module you will take your Midterm Exam or Exam 2.
Read the Midterm Exam or Exam 2 Information and Instructions page carefully and take note of any special submission guidelines.
Upon completion of this module, you will have:- Read and viewed the Midterm Exam or Exam 2 Information and Instructions page
- Scheduled your exam with the proctoring service [if applicable, delete if not needed]
- Post in the Midterm Exam or Exam 2 Q&A Discussion Forum - link provided below.
- Prepared for and submitted your Midterm Exam or Exam 2 [revise as needed]
- Uploaded your work in the Midterm Exam or Exam 2 Work Upload Assignment using the submission link below.
Attribution of image: ("Math, Numbers, Number image. Free for use." Pixabay.com. https://pixabay.com/photos/math-numbers-number-counting-5247958/)Adopting instructors: Edit the Midterm Exam or Exam 2 Information and Instructions page.
-
Imagine placing a plant in the ground one day and finding that it has doubled its height just a few days later. Although it may seem incredible, this can happen with certain types of bamboo species. These members of the grass family are the fastest-growing plants in the world. One species of bamboo has been observed to grow nearly 1.5 inches every hour (http://www.guinnessworldrecords.com/records-3000/fastest-growing-plant/). In a twenty-four hour period, this bamboo plant grows about 36 inches, or an incredible 3 feet! A constant rate of change, such as the growth cycle of this bamboo plant, is a linear function.
Recall from Functions and Function Notation (Section 3.2) that a function is a relation that assigns to every element in the domain exactly one element in the range. Linear functions are a specific type of function that can be used to model many real-world applications, such as plant growth over time. In this chapter, we will explore linear functions, their graphs, and how to relate them to data.
Image Caption: A bamboo forest in China (credit: "JFXie"/Flickr)
(Content & Image Source: Chapter 4 Introduction, Algebra and Trigonometry 2e, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:Section 4.1 Linear Equations in Two VariablesSection 4.2 Linear Functions- Write an linear equation in two variables (CLO1)
- Given the equations of two lines, determine whether their graphs are parallel or perpendicular. (CLO1)
- Write the equation of a line parallel or perpendicular to a given line. (CLO1)
- Represent a linear function. (CLO1)
- Determine whether a linear function is increasing, decreasing, or constant.(CLO1)
- Interpret slope as a rate of change.(CLO1)
- Write and interpret an equation for a linear function.(CLO3)
- Graph linear functions.(CLO1)
Section 4.3 Modeling with Linear Functions
- Build linear models from verbal descriptions.(CLO3)
- Model a set of data with a linear function.(CLO3)
Section 4.4 Systems of Linear Equations: Two Variables
- Solve systems of equations by graphing. (CLO1, CLO3)
- Solve systems of equations by substitution.(CLO1, CLO3)
- Solve systems of equations by addition.(CLO1, CLO3)
- Identify inconsistent systems of equations containing two variables.(CLO1, CLO3)
- Express the solution of a system of dependent equations containing two variables.(CLO1, CLO3)
To achieve these objectives:- Read the Module 4 Introduction (see above).
- Read Sections 4.1 - 4.4 of Chapter 4: Linear Functions in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 4 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 4 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 4 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 4 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
Digital photography has dramatically changed the nature of photography. No longer is an image etched in the emulsion on a roll of film. Instead, nearly every aspect of recording and manipulating images is now governed by mathematics. An image becomes a series of numbers, representing the characteristics of light striking an image sensor. When we open an image file, software on a camera or computer interprets the numbers and converts them to a visual image. Photo editing software uses complex polynomials to transform images, allowing us to manipulate the image in order to crop details, change the color palette, and add special effects. Inverse functions make it possible to convert from one file format to another. In this chapter, we will learn about these concepts and discover how mathematics can be used in such applications.
Image Caption: 35-mm film and SD cards, once the standard for capturing photographic images, has been made largely obsolete by digital photography. (credit “film”: modification of work by Horia Varlan; credit “memory cards”: modification of work by Paul Hudson)
(Content & Image Source: Chapter 5 Introduction, Algebra and Trigonometry, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:Section 5.1 Quadratic Functions
- Recognize characteristics of parabolas.
- Understand how the graph of a parabola is related to its quadratic function.
- Find the domain and range of a quadratic function.
- Determine and solve problems involving the minimum or maximum value of a quadratic function.
Section 5.2 Power Functions and Polynomial Functions
- Identify power functions.
- Identify end behavior of power functions.
- Identify polynomial functions.
- Identify the degree and leading coefficient of polynomial functions.
Section 5.3 Graphs of Polynomial Functions
- Recognize characteristics of graphs of polynomial functions.
- Use factoring to find zeros of polynomial functions.
- Identify zeros and their multiplicities.
- Determine end behavior.
- Understand the relationship between degree and turning points.
- Graph polynomial functions.
- Use the Intermediate Value Theorem.
Section 5.4 Dividing Polynomials
- Use long division to divide polynomials.
- Use synthetic division to divide polynomials.
Section 5.5 Zeros of Polynomial Functions
- Evaluate a polynomial using the Remainder Theorem.
- Use the Factor Theorem to solve a polynomial equation.
- Use the Rational Zero Theorem to find rational zeros.
- Find zeros of a polynomial function.
- Use the Linear Factorization Theorem to find polynomials with given zeros.
- Use Descartes’ Rule of Signs.
- Solve real-world applications of polynomial equations
Section 5.6 Rational Functions
- Use arrow notation.
- Solve applied problems involving rational functions.
- Find the domains of rational functions.
- Identify vertical asymptotes.
- Identify horizontal asymptotes.
- Graph rational functions.
To achieve these objectives:- Read the Module 5 Introduction (see above).
- Read Sections 5.1 - 5.6 of Chapter 5: Polynomial and Rational Functions in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 5 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 5 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 5 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 5 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
In this module you will take your Exam 2 or Exam 3. [revise as needed]
Read the Exam 2 or Exam 3 Information and Instructions page carefully and take note of any special submission guidelines.
Upon completion of this module, you will have:- Read and viewed the Exam 2 or Exam 3 Information and Instructions page
- Scheduled your exam with the proctoring service [if applicable, delete if not needed]
- Post in the Exam 2 or Exam 3 Q&A Discussion Forum - link provided below.
- Prepared for and submitted your Exam 2 or Exam 3 [revise as needed]
- Uploaded your work in the Exam 2 or Exam 3 Work Upload Assignment using the submission link below.
Attribution of image: ("Math, Numbers, Number image. Free for use." Pixabay.com. https://pixabay.com/photos/math-numbers-number-counting-5247958/)
Adopting instructors: Edit the Exam 2 or Exam 3 Information and Instructions page.
-
Focus in on a square centimeter of your skin. Look closer. Closer still. If you could look closely enough, you would see hundreds of thousands of microscopic organisms. They are bacteria, and they are not only on your skin, but in your mouth, nose, and even your intestines. In fact, the bacterial cells in your body at any given moment outnumber your own cells. But that is no reason to feel bad about yourself. While some bacteria can cause illness, many are healthy and even essential to the body.
Bacteria commonly reproduce through a process called binary fission, during which one bacterial cell splits into two. When conditions are right, bacteria can reproduce very quickly. Unlike humans and other complex organisms, the time required to form a new generation of bacteria is often a matter of minutes or hours, as opposed to days or years (Todar, PhD, Kenneth. Todar's Online Textbook of Bacteriology. http://textbookofbacteriology.net/growth_3.html).
For simplicity’s sake, suppose we begin with a culture of one bacterial cell that can divide every hour. Table 1 below shows the number of bacterial cells at the end of each subsequent hour. We would see that the single bacterial cell leads to over one thousand bacterial cells in just ten hours! And if we were to extrapolate the table to twenty-four hours, we would have over 16 million!
Table 1 Hour 0 1 2 3 4 5 6 7 8 9 10 Bacteria 1 2 4 8 16 32 64 128 256 512 1024
In this chapter, we will explore exponential functions, which can be used for, among other things, modeling growth patterns such as those found in bacteria. We will also investigate logarithmic functions, which are closely related to exponential functions. Both types of functions have numerous real-world applications when it comes to modeling and interpreting data.Image Caption: Electron micrograph of E.Coli bacteria (credit: “Mattosaurus,” Wikimedia Commons)(Content & Image Source: Chapter 6 Introduction, Algebra and Trigonometry 2e, Jay Abramson, OpenStax, CC BY 4.0 License)
Upon completion of this module, you will be able to:
Section 6.1 Exponential Functions
Section 6.2 Graphs of Exponential Functions- Evaluate exponential functions.
- Find the equation of an exponential function.
- Use compound interest formulas.
- Evaluating Functions with Base e.
- Graph exponential functions.
- Graph exponential functions using transformations.
Section 6.3 Logarithmic FunctionsSection 6.4 Graphs of Logarithmic Functions- Convert from logarithmic to exponential form.
- Convert from exponential to logarithmic form.
- Evaluate logarithms.
- Use common logarithms.
- Use natural logarithms.
Section 6.5 Logarithmic Properties- Identify the domain of a logarithmic function.
- Graph logarithmic functions.
- Graphing Transformations of Logarithmic Functions.
Section 6.6 Exponential and Logarithmic Equations- Use the product rule for logarithms.
- Use the quotient rule for logarithms.
- Use the power rule for logarithms.
- Expand logarithmic expressions.
- Condense logarithmic expressions.
- Use the change-of-base formula for logarithms.
Section 6.7 Exponential and Logarithmic Models- Use like bases to solve exponential equations.
- Use logarithms to solve exponential equations.
- Use the definition of a logarithm to solve logarithmic equations.
- Use the one-to-one property of logarithms to solve logarithmic equations.
- Solve applied problems involving exponential and logarithmic equations.
- Model exponential growth and decay.
- Use Newton’s Law of Cooling.
- Use logistic-growth models.
- Choose an appropriate model for data.
- Express an exponential model in base e.
To achieve these objectives:- Read the Module 6 Introduction (see above).
- Read Sections 6.1 - 6.7 of Chapter 6: Exponential and Logarithmic Functions in College Algebra (links to each Section provided below)
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- At the end of each Section there is a list of Key Concepts, Section Exercises, and a Glossary of terms
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- Practice the problems on the Chapter 6 Review Exercises, checking the solutions provided (link provided below)
- View the Chapter 6 Practice Test (link provided below)
- Complete the MyOpenMath Quiz for Chapter 6 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 6 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
In this module you will take your Final Exam.
Read the Final Exam Information and Instructions page carefully and take note of any special submission guidelines.
Upon completion of this module, you will have:- Read and viewed the Final Exam Information and Instructions page
- Scheduled your exam with the proctoring service [if applicable, delete if not needed]
- Post in the Final Exam Q&A Discussion Forum - link provided below.
- Prepared for and submitted your Final Exam [revise as needed]
- Uploaded your work in the Final Exam Work Upload Assignment using the submission link below.
Attribution of image: ("Math, Numbers, Number image. Free for use." Pixabay.com. https://pixabay.com/photos/math-numbers-number-counting-5247958/)
Adopting instructors: Edit the Final Exam Information and Instructions page.